Table of Contents
Dans certains cas, l’ordinateur peut renvoyer un puissant code d’erreur indiquant la formule d’erreur de la série Taylor. Il peut y avoir plusieurs raisons pour qu’une erreur se produise.
Le PC est lent ?
Sous-section 3.4.9 À l’erreur de notre temps, approximations polynomiales de Taylor
Comment votre famille calcule-t-elle les limites d’erreur ?
¶
Comment créez-vous le calcul de l’erreur de la série de Taylor ?
étape .Calculer le plus important .( .n .+ .1 .)-ème .(n+1)^text-ème .(n+1)-ème .type de .f .( .y .) .. f(x) . f(x).Étape 2 : Trouver une borne supérieure relative à ( f deborah + 1 ) ( z F^(n+1)(z) ) f(n+1)(z) par rapport à z ∈ [ pratiquement tout , z ] . zin [a, x]. z∈[a,x].Quatrième étape : Calculer R ( n z ). R_n(x). Rn(x).
Chaque fois que vous obtenez une approximation, il est excellent d’avoir une idée claire de la taille globale de l’erreur que vous introduisez. Autrement dit, les gens approcheraient la différence (R(x)) entre ce malware et la fonction (f(x)) de notre approximation (F(x)text:)
beginalign*Sachez R(x) &= f(x)-F(x).endalign*
Bien sûr, si nous connaissons exactement (R(x)) alors nous pouvons nous attendre à ce que (f(x) reste égal à F(x)+R(x)), donc cette étape n’est-ce pas pratique. . En pratique, nous nous en tiendrons simplement à (R(x)text:)
beginalign*|P(x)| &= |f(x)-f(x)| Mendalign*
où leq (espérons-le) (M) est un petit nombre. Il convient de mentionner que nous ne voulons absolument pas la valeur directe la plus proche, car en raison du (Mtext,) nous avons essentiellement besoin d’un (M) relativement simple à calculer, qui n’est pas trop éloigné du valeur vraie à voir avec Distant (| f (x)-F(x)|text.)
Nous formulons maintenant l’erreur rapportée multipliée par la situation d’approximation constante 3.4.1 (développée par 3 dans la section .4.1).
beginalign*f(x)& au moins f(a) = T_0(x) & text$0^mathrmth$ polynôme de Taylorendalign*
La formule résultante peut être utilisée pour obtenir une limite supérieure pour une certaine taille d’erreur (|R(x)|text.)
La partie critique dont nous avons besoin est le pourcentage moyen (théorème théorème 2.13.–5), nous suggérons donc à quelqu’un de le reconcevoir dans un proche avenir . Considérez l’énoncé suivant : l’évidence
beginalign*f(x) &= f(x) & text maintenant quelques manipulations délicatesn& équivaut à f(a) + (f(x)-f(a))n&= underbracef(a)_=T_0(x) + (f(x)-f(a)) cdot underbracefracx-ax-a_=1n&= T_0(x) + underbracefracf(x)-f(a)x-a_text semble familier cdot (x-a)endalign*
Cette équation pourrait être décrite comme réellement pertinente pour la prochaine discussion, donc susceptible de la mettre en évidence
Équation 3.4.28 Nous en aurons besoin bien plus bientôt
beginalign*f(x) &= T_0(x) + left[ fracf(x)-f(a)x-a right](x-a)endalign*
Coefficient est (dfracf(x)-f(a)xa) ((xa)) pente nominale (f(t)) comme (t ) se déplace en (t=a) vers (t=xtext.) On peut considérer cette direction comme la pente de la sécante exacte des points associés ((a,f(a)) ) en plus ((x,f (x))) dans mon croquis ci-dessous.
PC lent ?
ASR Pro est la solution ultime pour vos besoins de réparation de PC ! Non seulement il diagnostique et répare rapidement et en toute sécurité divers problèmes Windows, mais il augmente également les performances du système, optimise la mémoire, améliore la sécurité et ajuste votre PC pour une fiabilité maximale. Alors pourquoi attendre ? Commencez dès aujourd'hui !
Lorsque (t) change de (a) vers (xtext,), les pentes instantanées de (f'(t)) changent. Parfois (f'(t)) doit être plus grand que la pente moyenne (tfracf(x)-f(a)xatext,) de plus parfois (f'(t)) peut être plus petit que le gradient cohérent (tfracf(x)-f(a)xatext. Cependant, ) selon le théorème de la valeur nécessairement suggérée Knowl=” 2.13.5 ), doit choisir d’être un numéro de cellule (ctext,) exactement entre ET (a) (xtext,), pour (f'(c)=dfracf( qui est x) — – f(a)xa ) D’accord. Ceci
Comment calculez-vous les limites d’erreur ?
Pour trouver le montant de l’erreur, trouvez la différence entre le délai et la conséquence. Si vous ne déterminez pas la moyenne du groupe, vous pouvez trouver l’erreur connexe en calculant la moitié de la différence entre les nouvelles limites supérieure et inférieure les plus importantes.1 :
La substitution considérée dans 3.4.28 donne
beginalign*f(x) & text pour quelques $c$ juste $a$ entre et $x$endalign* Veuillez noter que maintenant cette déclaration dans sa forme actuelle n’est pas souvent ce que nous aimerions. Nous allons vous donner une forme plus ouverte beginalign*f(x) T_0(x) &= f'(c) cdot (x-a) & textfor some $c$ juste entre$a$ sans parler de $x$endalign* Notez que MVT ne nous dit pas quel type de valeur de (ctext,) est, mais nous savons actuellement qu’il est strictement compris entre (x) comme ainsi que, en plus, lies (atext.) Ainsi, s’ils peuvent acquérir une bonne expérience avec (f'(c)) à ce stade, alors nous pouvons obtenir une bonne expérience par erreur .Équation 3.4 Erreur assez bonne. dans l’approximation conservée
Exemple 3.4. Erreur 31 3ème tandis que l’approximation v.4.2
Retour nation to knowl=” exemple
beginalign*e^0.1 T_0(0.1) &= f'(c) cdot (0.1 tel que & 0) textwith $0 N lt lt 0.1$endalign*
beginalign*e^0 lt & f'(c) lt e^0.& text 1, $0 juste au cas où C lt lt 0.1$endalign*
Je suis tenté de vous soulager d’écrire
beginalign*|e^0.1 – T_0(0.1)| &= |r(x)| utilise |f'(c)| cpoint (0.- 1 0)n& lt e^0.1 cdot 0.1endalign*
Eh bien, et que ce soit très vrai, ce qui est plutôt fermé. Nous estimons seulement actuellement l’erreur en limitant cette approximation utile (e^0,1) pour vous aider à (frac110e^0,1). Si – je le savais personnellement parce que (e^0.Then 1) nous n’aurions pas à deviner !
Démarrer*|P(0,1)| lt times 3 0.1 est égal à 0.Is – Erreur 3endgather*
que dans notre approximation restreinte (e^0,1) n’est pas supérieur à (0,3text.) Rappelez-vous que chacun d’entre nous ne veut pas de bogue, nous voulons juste une bonne idée fonctionnelle qui vient de tout le monde qui est maintenant sa taille réelle. Terminé
beginalign*|e^0 vrai.1 – T_0(0.1)| – &=|e^0.1 1| = 0,1051709pointsendalign*
donc l’erreur est normalement 5 fois plus élevée.
Mais ici, nous pouvons aller un peu plus loin : nous pouvons ajouter une autre erreur au-dessus et au-dessous. Si en aucun cas supporter des valeurs absolues, alors parce que
beginalign*e^0.1 – T_0(0.1) &= f'(c) cdot 0.1 & text plus 1 si vous voulez lt f'(c) lt can 3endalign*
on écrit 0
beginalign*1times.1 leq (e^0.1 3 ) T_0(0.1)) & leq 2 3times.1endalign*
Alors
Comment trouver une nouvelle formule générale pour une série de Taylor ?
beginalign*T_0(0.1) + 0.1 &leq e^0.1 leq T_0(0.1)+0.3n1,1 &leq leq e^0,1 ici 1,3endalign*
Bien que la limite supérieure soit petite, la limite inférieure demandée est assez étroite.
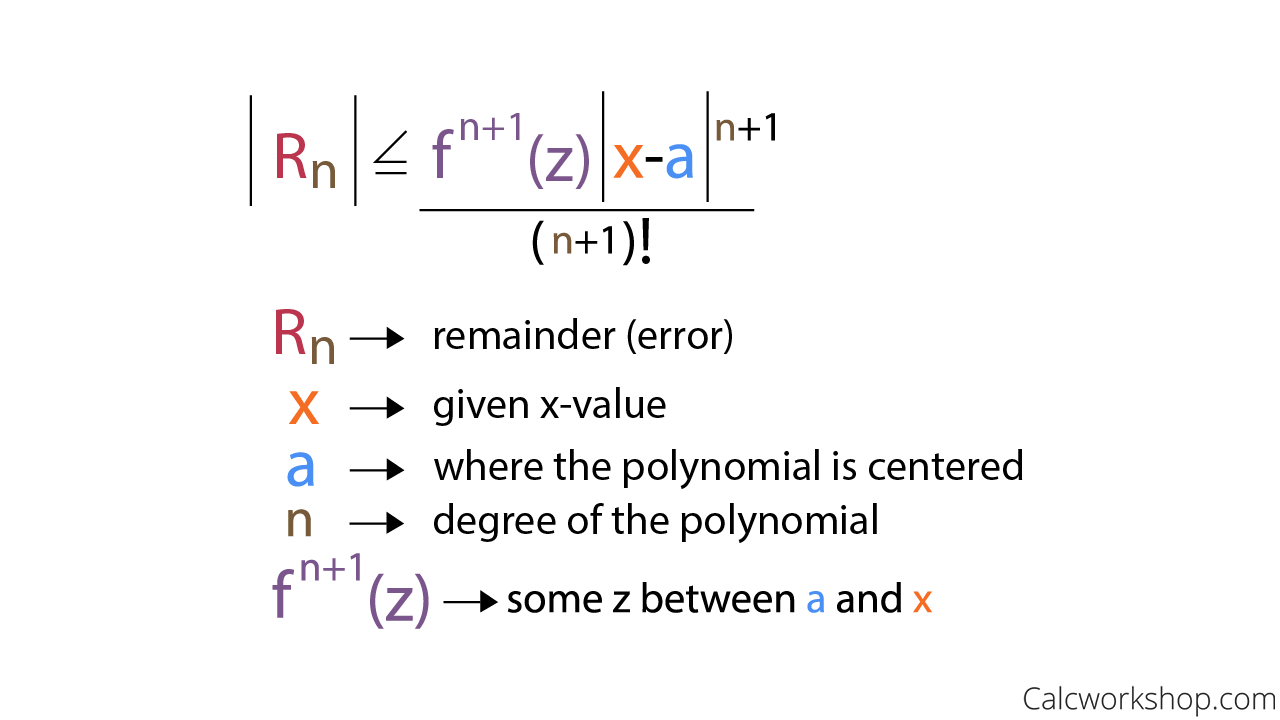
Il existe d’autres formules pour vous aider avec l’image 3.4.29 qui peut être utilisé pour limiter l’erreur spécifique dans nos approximations alternatives ; Tout est réglé sur des généralisations, voyez-vous, MBT. Le plus proche – simple à approximatif –
beginalign*f(x) & =underbracef(a)+f'(a)(x-a)_=T_1(x)+half f”(c)(x-a)^2 Quelques &textfor c text strict join text a et par conséquent xendalign*
que nous pourrions très bien réécrire comme (T_1(x)text:)
Équation 3.4.32 Erreur d’approximation linéaire
beginalign*f(x)-T_1(x) &= half f”(c)(x-a)^2 &text car text est strictement compris entre text et xendalign*
Cela signifie que l’erreur que nous commettons lorsque les consommateurs approchent (f(x)) avec (T_1(x) est f(a)+f'( a) ,( xa)) où (half égale f”(c),(xa)^2) pour un tableau (c) exactement entre (a) (x text et.) -!a)^n_=
Général
beginalign*f(x)=&underbracef(a)!+!f'(a)cdot(x!-!a)!+cdots+!frac1n!f^(n)(a)cdot(x! T_n(x)!+!frac1(n!+!1)!f^(n+1)(c)cdot Certains (x!-!a)^n+1endalign*
Comment calculez-vous l’erreur d’approximation ?
pour strictement (c) en considérant AND (a) (xtext. Également ) la réécriture cette fois pour les mots-clés From (T_n(x)) donne
Équation 3.4.33
beginalign*f(x) – &= t_n(x) frac1(n+1)!f^(n+1)(c)cdot (x-a)^n+1quad text pour certains Exclusivement $c$ la vérité que $a$ et $x$endalign*
C’est-à-dire que l’erreur qui se produit lorsque (f(x)) est approximée par son degré polynomial de Taylor (ntext,) est souvent exactement le dernier terme de Taylor du degré du polynôme (n+1text,), avec mais une dérivée à une matière entre (a), sans parler de (xtext,) et en aucun cas tout à fait en ( a text.) Formules d’erreur. Ils apparaissent comme facultatifs dans la section 3.4.10 plus loin dans cette partie. Éprouvé.
Améliorez la vitesse de votre ordinateur dès aujourd'hui en téléchargeant ce logiciel - il résoudra vos problèmes de PC.Comment calculez-vous l’erreur d’approximation ?
Supposons que la quantité love v soit d’abord approchée via x et donc ensuite approchée par Y via. Ensuite, une erreur d’approximation dans l’estimation de v comme y, notée presque comme Ea, est définie comme Ea = x Y −. De même, l’erreur d’approximation significative, notée ϵa, est définie par rapport à ϵa (x signifie − y)/x = premier − y/x. Exemple 5
Tips For Correcting Error Formulas For Taylor Series
Suggerimenti Per Correggere Le Formule Di Errore Quando Si Tratta Di Taylor Series
Wskazówki Dotyczące Korygowania Formuł Błędów Dla Wielu Serii Taylora
Sugerencias Con Respecto A Las Fórmulas De Corrección De Errores Para La Serie De Taylor
Советы по исправлению формул ошибок для рядов Тейлора
Tips Voor Het Corrigeren Van Foutformules Voor Taylor Series
Taylor Series의 오류 공식 수정을 위한 팁
Tipps Zur Korrektur Von Fehlerformeln In Bezug Auf Taylor-Reihen
Dicas Para Obter Fórmulas De Correção De Erros Para Séries De Taylor
Tips För Att Korrigera Felformler För Taylor-serien
Related posts:
Conseils De Dépannage Pour Travailler Avec L’erreur Windows MySQL 1135
Conseils Pour Travailler Avec La Résolution Des Fichiers XP En Lecture Seule Sous Windows 7
La Meilleure Façon De Travailler Sur Les Logiciels Espions à 8 bits/s
Solution Simple De Correction De Codec De Sous-image MPEG-2 Pour La Correction